AES简介
高级加密标准(AES,Advanced Encryption Standard),是最为常见的加密算法,所谓对称加密就是使用相同的密钥进行加密和解密
加密流程如下
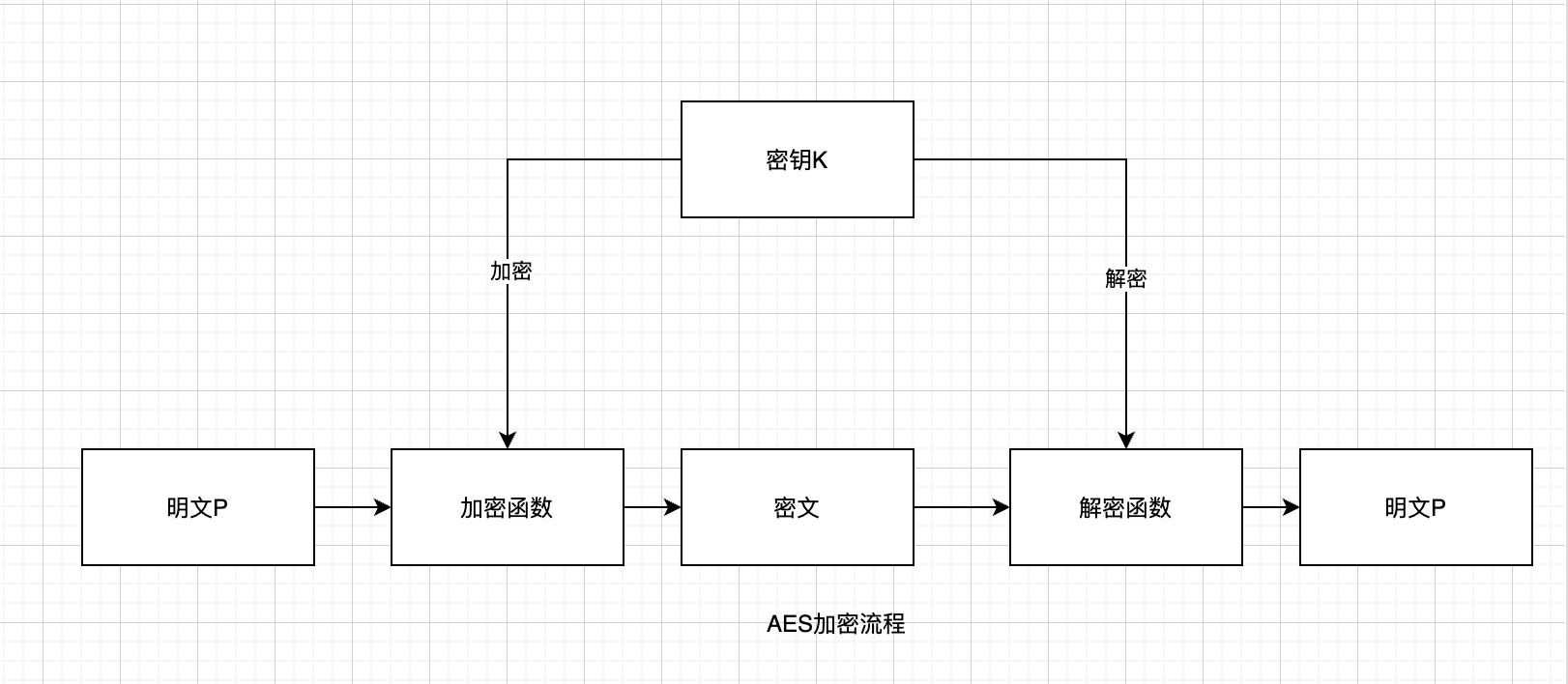
密钥可以面对面约定或者使用非对称加密算法加密之后进行传输。
AES为分组密码,分组密码也就是把明文分成组,每组长度相等。每次加密一组数据,直到加密完整个明文。在AES标准规范中,分组长度只能是128位,也就是说,每个分组为16个字节(每个字节8位)。密钥的长度可以使用128位、192位或256位。密钥的长度不同,推荐加密轮数也不同,如下表所示:
| AES | 密钥长度(32位比特字) | 分组长度(32位比特字) | 加密轮数 |
|---|---|---|---|
| AES-128 | 4 | 4 | 10 |
| AES-192 | 6 | 4 | 12 |
| AES-256 | 8 | 4 | 14 |
所谓
AES-128也就是密钥的长度为128位,加密轮数为10轮。也就是执行一个加密函数十次。但是前九轮执行顺序相同,第十实现才有所不同。解密过程是加密过程的逆过程,调用解密函数
加密前九轮每一轮的操作顺序为字节代换、行位移,列位移、列混合,轮密钥加。
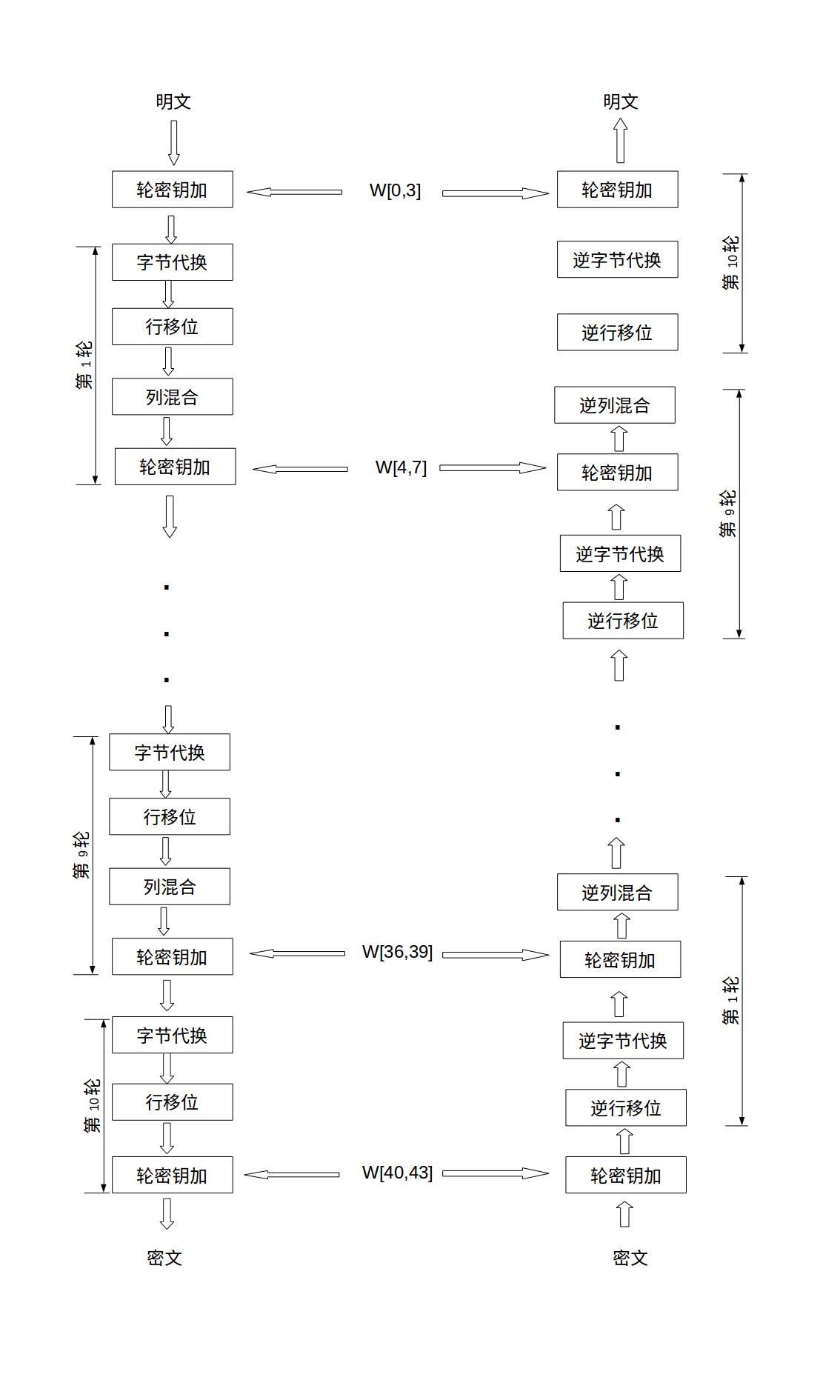
字节代换和逆字节代换
AES的字节代换其实就是一个简单的查表操作。AES定义了一个S盒和一个逆S盒。
状态矩阵中的元素按照下面的方式映射为一个新的字节:把该字节的高4位作为行值,低4位作为列值,取出S盒或者逆S盒中对应的行的元素作为输出。
行移位
行移位是一个简单的左循环移位操作。当密钥长度为128比特时,状态矩阵的第0行左移0字节,第1行左移1字节,第2行左移2字节,第3行左移3字节。
行移位的逆变换是将状态矩阵中的每一行执行相反的移位操作,例如AES-128中,状态矩阵的第0行右移0字节,第1行右移1字节,第2行右移2字节,第3行右移3字节。
列混合
列混合变换是通过矩阵相乘来实现的,经行移位后的状态矩阵与固定的矩阵相乘,得到混淆后的状态矩阵。
轮密钥加
轮密钥加是将128位轮密钥Ki同状态矩阵中的数据进行逐位异或操作,如下图所示。其中,密钥Ki中每个字W[4i],W[4i+1],W[4i+2],W[4i+3]为32位比特字,包含4个字节,他们的生成算法下面在下面介绍。轮密钥加过程可以看成是字逐位异或的结果,也可以看成字节级别或者位级别的操作。也就是说,可以看成S0 S1 S2 S3 组成的32位字与W[4i]的异或运算。
轮密钥加的逆运算同正向的轮密钥加运算完全一致,这是因为异或的逆操作是其自身。轮密钥加非常简单,但却能够影响S数组中的每一位。
以上为每次轮函数操作流程,调用轮函数之前我们先进行的是对密钥进行拓展。
密钥扩展
- 先将密钥放入4X4矩阵中,获取每一列组成新的矩阵W1,W2,W3,W4。
- 扩充矩阵矩阵到44列。
分组明文补全策略
使用PKCS5、PKCS7和NOPADDING三种模式进行补全。PKCS5是指分组数据缺少几个字节,就在数据的末尾填充几个字节的几,比如缺少5个字节,就在末尾填充5个字节的5。PKCS7是指分组数据缺少几个字节,就在数据的末尾填充几个字节的0,比如缺少7个字节,就在末尾填充7个字节的0。NoPadding是指不需要填充,也就是说数据的发送方肯定会保证最后一段数据也正好是16个字节。那如果在PKCS5模式下,最后一段数据的内容刚好就是16个16怎么办?那解密端就不知道这一段数据到底是有效数据还是填充数据了,因此对于这种情况,PKCS5模式会自动帮我们在最后一段数据后再添加16个字节的数据,而且填充数据也是16个16,这样解密段就能知道谁是有效数据谁是填充数据了。PKCS7最后一段数据的内容是16个0,也是同样的道理。解密端需要使用和加密端同样的Padding模式,才能准确的识别有效数据和填充数据。我们开发通常采用PKCS7 Padding模式。
注在17年做该加密方案时候,貌似iOS端使用PKCS7和后端进行加解密开发时候无法成功,换成PKCS7才可以。
CBC模式
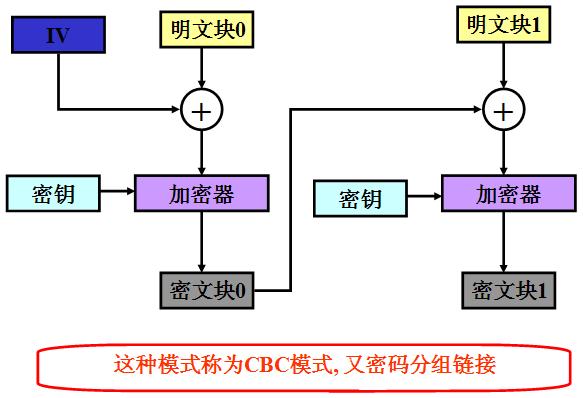
RSA加解密流程
第一步:生成密钥对,即公钥和私钥。
1:随机找两个质数 P 和 Q ,P 与 Q 越大,越安全。
比如 P = 67 ,Q = 71。计算他们的乘积 n = P * Q = 4757 ,转化为二进为 1001010010101,该加密算法即为 13 位,实际算法是 1024 位 或 2048 位,位数越长,算法越难被破解。
2:计算 n 的欧拉函数 φ(n)。
φ(n) 表示在小于等于 n 的正整数之中,与 n 构成互质关系的数的个数。例如:在 1 到 8 之中,与 8 形成互质关系的是1、3、5、7,所以 φ(n) = 4。 如果 n = P * Q,P 与 Q 均为质数,则 φ(n) = φ(P * Q)= φ(P - 1)φ(Q - 1) = (P - 1)(Q - 1) 。 本例中 φ(n) = 66 * 70 = 4620,这里记为 m, m = φ(n) = 4620
3:随机选择一个整数 e,条件是1< e < m,且 e 与 m 互质。
公约数只有 1 的两个整数,叫做互质整数,这里我们随机选择 e = 101 请注意不要选择 4619,如果选这个,则公钥和私钥将变得相同。
4:有一个整数 d,可以使得 e*d 除以 m 的余数为 1。
即找一个整数 d,使得 (e * d ) % m = 1。 等价于 e * d - 1 = y * m ( y 为整数) 找到 d ,实质就是对下面二元一次方程求解。 e * x - m * y =1 ,其中 e = 101,m = 4620 101x - 4620y =1 这个方程可以用“扩展欧几里得算法”求解,此处省略具体过程。 总之算出一组整数解(x,y )= ( 1601,35),即 d = 1601。 到此密钥对生成完毕。不同的 e 生成不同的 d,因此可以生成多个密钥对。
本例中公钥为 (n,e) = (4757 , 101),私钥为 (n,d) = (4757 ,1601) ,仅(n,e) = (4757 , 101) 是公开的,其余数字均不公开。可以想像如果只有 n 和 e,如何推导出 d,目前只能靠暴力破解,位数越长,暴力破解的时间越长。
第二步:加密生成密文 。
比如甲向乙发送汉字“中”,就要使用乙的公钥加密汉字 “中”, 以 utf-8 方式编码为 [e4 b8 ad],转为 10 进制为 [228,184,173]。要想使用公钥(n,e) = (4757 , 101)加密,要求被加密的数字必须小于 n,被加密的数字必须是整数,字符串可以取 ascii 值或unicode值,因此将“中”字折为三个字节 [228,184,173],分别对三个字节加密。 假设 a 为明文,b 为密文,则按下列公式计算出 b
1 | a^e % n = b |
计算 [228,184,173]的密文:
228^101 % 4757 = 4296
184^101 % 4757 = 2458
173^101 % 4757 = 3263
即 [228,184,173]加密后得到密文 [4296,2458,3263] ,如果没有私钥 d ,神仙也无法从 [4296,2458,3263]中恢复 [228,184,173]。
乙收到密文 [4296,2458,3263],并用自己的私钥(n,d) = (4757 ,1601) 解密。解密公式如下: 假设 a 为明文,b 为密文,则按下列公式计算出 a
1 | a^d % n = b |
密文 [4296,2458,3263]的明文如下:
4296^1601% 4757 = 228
2458^1601% 4757 = 184
3263^1601% 4757 = 173
即密文 [4296,2458,3263] 解密后得到 [228,184,173] 将[228,184,173] 再按 utf-8 解码为汉字 “中”,至此解密完毕。
加密和解密的过程使用了费尔马小定理的两种等价的描述。